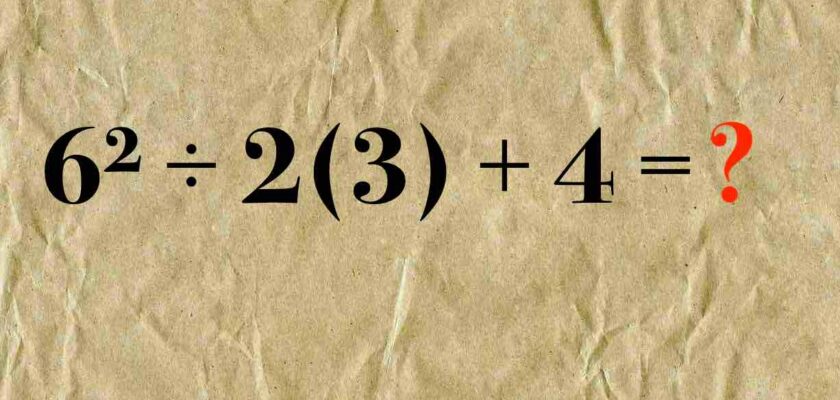Voici un problème mathématique apparemment simple qui crée une réelle polémique en ligne pour une raison inattendue.
Arriverez-vous à le résoudre ? Et surtout, de quel côté du débat vous situerez-vous ?
De nombreuses personnes abordent ce type de problème en appliquant des règles apprises de manière académique.
Cependant, nous faisons parfois l’erreur de croire qu’il n’existe qu’une seule manière de parvenir à la solution, notamment en ce qui concerne « l’ordre des opérations ». Si nous examinons attentivement ce problème, nous pourrions découvrir la réponse la plus logique.
Essayez de résoudre l’expression ci-dessous avant de poursuivre :
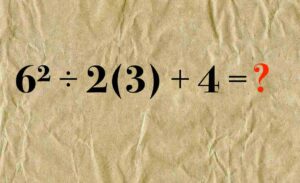6² ÷ 2(3) + 4 = ?
À première vue, cela semble simple, n’est-ce pas ? Mais les règles de « l’ordre des opérations », connues sous l’acronyme PEMDAS (Parenthèses, Exposants, Multiplication et Division, Addition et Soustraction), peuvent prêter à confusion dans certains cas.
Rappelons que lorsque des opérations ont la même priorité, elles doivent être exécutées de gauche à droite.
De nombreuses personnes interprètent l’expression « 2(3) » comme une multiplication directe et trouvent la solution suivante en appliquant l’ordre PEMDAS :
6² ÷ 2 × 3 + 4 = 58
Ainsi, la réponse obtenue est 58, et une calculatrice classique produira la même réponse.
Cependant, d’autres personnes abordent le problème différemment, en considérant que « 2(3) » pourrait avoir une priorité implicite supérieure. En résolvant ainsi, et en poursuivant de gauche à droite, certains obtiennent :
6² ÷ 6 + 4 = 10
Cette approche donne donc une réponse de 10.
Alors, quelle est la bonne réponse ?
La réponse correcte est 58. Selon l’explication de Dave Burton sur Quora, la notation utilisée ici n’est pas standard et prête à confusion, ce qui rend l’expression ambiguë. « 2(3) » n’implique aucune priorité particulière ; il s’agit d’une simple multiplication, et non d’une modification de l’ordre des opérations.
Pour illustrer l’importance de la clarté, l’animateur YouTube Presh Talwakar compare cette ambiguïté à celle de certains énoncés en langue française. Par exemple :
« J’ai vu l’homme avec des jumelles. »
Cela pourrait signifier (a) que vous avez utilisé des jumelles pour voir l’homme, ou (b) que l’homme lui-même avait des jumelles.
En somme, le débat ne remet pas en question les règles mathématiques en elles-mêmes, mais plutôt l’ambiguïté de la notation utilisée.
